Оптимальное управление порожними вагонами при условии задания агрегированных транспортных грузопотоков.

Пусть имеется сеть узлов Р= {р_1, р_2…р_N} производства и потребления продукции . Известны планы грузопотоков за период Т (месяц, квартал), А _{i j} – плановое количество вагонов с продукцией, которые нужно отправить в течение периода Т из пункта (производства) i пункт (потребления) j . Также известны времена перегона груженых и пустых вагонов и стоимость перегона .

Простейший вариант управления вагонным парком заключается в том, что мы циклически отправляем порожние вагоны обратно на погрузку в тот же пункт производства, откуда они пришли (если, конечно, нет обратного грузопотока, с помощью которого можно их загрузить) . Если существует несколько пунктов производства (продукция может быть совершенно разной – главное чтобы её можно было грузить в те же вагоны), то простейшее управление может быть неоптимальным, например:

потребление 1 производство 2

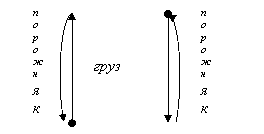
производство 1 потребление 2

Рис. 1 Простейшее решение

потребление 1 порожняк производство 2

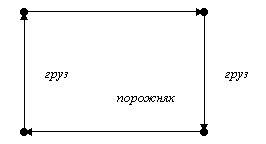
производство 1 потребление 2

Рис. 2 Альтернативное решение

В зависимости от времен и стоимостей перегона вариант перевозок на рис . 2 может оказаться более выгодным, чем простейшее решение . То есть появляется смысл в постановке задач(и) оптимального управления порожняком – определение маршрутов движения порожняка с целью его минимизации . Можно также поставить задачу определения минимального количества вагонов, которые необходимы и достаточны для выполнения перевозок в соответствии с заданным агрегированным планом грузоперевозок А _{i j .} Такие задачи, по-видимому, невозможно поставить, не рассматривая систему в динамике . Так взаимоувязка маршрутов порожняка зависит от времен перегона груженых и порожних вагонов и, поэтому может быть осуществлена более естественно в рамках динамической модели .

Модель, которую мы будем строить является некоторым расширением динамической транспортной задачи . Разделим период Т на интервалы (дни) и введем время t=0,1.2…T .

В отличие от классической ДТЗ у нас здесь нет функций потребления и производства порожних вагонов . Так как в данном случае мы имеем только агрегированные планы грузопотока и на основе них можно построить только агрегированные планы ‘потребления’ и ‘производства’ порожних вагонов .

Введем обозначения:

U _{i j} (t) – количество пустых убывших вагонов из пункта i в пункт j в момент времени t

V _{i j}(t) – количество груженых вагонов, убывших из пункта i в пункт j в момент времени t

Будем считать, что вагоны грузятся непосредственно перед отправкой и выгружаются сразу после прибытия . Поэтому V _{i j} также участвует в балансе порожних вагонов .

х_i (t) – количество порожних вагонов в пункте i в момент времени t

Имеем балансовые соотношения запасов порожних вагонов

N N N N ^

х_i (t) = х_i (t) – Σ U _{i j} (t-1) + Σ U _ji (t-1-τ_ij) – Σ V _{i j} (t-1) + Σ V _ji(t-1-τ_ij--ө_j-μ_i) (1)

j=1 j=1 j=1 j=1

^

здесь τ_ij и τ_ij - времена перегонов порожних и груженых вагонов соответственно .

ө_j –время погрузки в пункте j

μ_i –время выгрузки в пункте i

Кроме того нам известно, что

Т

Σ V _{i j} (t)= А _{i j} (2)

t=0

То есть сумма всех перевозок из пункта i в пункт j определяется агрегированным планом грузопотока .

Ещё нам может быть известно либо распределение порожних вагонов по пунктам сети в

N

момент времени 0, т . е . все х_i(0), либо хотя бы их общее количество Σ х_i(0)=M

i=1

Или можно поставить сначала задачу минимизации вагонного парка:

N

Σ х_i(0) ð min

i=1

при условии (1) и (2) и условиях неотрицательности всех переменных

Определив минимальное количество вагонов можно дать ему определенный запас и решать задачу по минимизации стоимости пробега порожних вагонов и максимизации дохода от перевоза груженых вагонов

^

Σ C _{i j} V _{i j}(t) - Σ C _{i j} U _{i j} (t) ð max

i,j . t i,j . t

и другие аналогичные задачи.

В результате решения задачи получаются не только маршруты и количество вагонов перегоняемого порожняка, но и детальная разбивка потока груженых вагонов по дням . Это может являться основой, нулевым приближением детального рабочего плана перевозок . После его уточнения с помощью других процедур, детальный план перевозок можно подставить в модель уже не в качестве переменных, а как исходные данные, и таким образом уточнить маршруты порожняка с помощью нового пересчета .

Поскольку в решении исходной задачи, как уже говорилось, получается детальная разбивка потока груженых вагонов по дням, то можно поставить задачу сделать этот поток как можно более равномерным .

Литература .

Динамическая транспортная задача с задержками / С . Л . Блюмин, П . А . Козлов, С . П . Миловидов // А втоматика и телемеханика . – 1984 . – № 5 .