Система
автоматизированного управления грузопотоками.
П.А. Козлов,
А.С. Мишарин.
Введение. В связи с развитием
рыночной экономики произошло резкое усложнение функций управления на
железнодорожном транспорте. Если раньше основная задача железных дорог формулировалась
как «перевозки», то теперь это – «транспортное обслуживание». Разница между
ними следующая. При взаимодействии транспорта и производства возникают так
называемые «стыковые потери». Предприятия создают резервы перерабатывающей
способности грузовых фронтов, складов, содержат дополнительные пути, вагоны,
локомотивы, штат. Из-за несвоевременного подвода порожняка и грузов простаивает
оборудование. Так вот при первой задаче стыковые потери относились на
производство, а при второй – на железные дороги. Транспорт во втором случае
старается обеспечить надежные и эффективные транспортные связи между
поставщиками и потребителями, то есть сделать территориально распределенную
производственную систему высокоорганизованной. Теперь нужно не просто привезти груз
(допустим, выдержав срок доставки), а осуществлять транспортное обслуживание по
различным классам качества, минимизируя стыковые потери. Ранее эта задача не
могла ставиться из-за чрезвычайной перегрузки железных дорог. Поэтому
качественное транспортное обслуживание с минимальными резервами не может быть
эффективно осуществлено без автоматизации управления.
Управление
на железнодорожном транспорте можно разделить на два класса [1]:
Первый – это оптимизация
технологического процесса работы железных дорог - оптимизация сменно-суточного планирования,
выбор очередности и характера выполнения технологических операций. Это позволит
улучшить использование технических средств и сократить внутренние затраты.
Второй – это управление
грузопотоками для обеспечения нужного класса транспортного обслуживания, что
позволит сократить стыковые потери и заработать железным дорогам дополнительные
средства. Если говорить об управлении потоками, то существует три их типа:
управление грузопотоками, вагонопотоками и поездопотоками. Для выполнения
задачи «перевозки» достаточно было двух последних. В рыночных условиях на
первое место выходит управление грузопотоками [1].
Необходимо
также отметить, что резко усложнилась задача управления потоками порожняка.
Во-первых, теперь есть вагоны «свои» и «чужие», во-вторых, вагоны годятся под
тот или иной груз, в-третьих, транспортное обслуживание предполагает подвод
требуемых вагонов в требуемом ритме.
В рыночных условиях резко
возросла динамика экономических, а значит, и транспортных связей. Находить
оптимальные или близкие к нему решения по управления грузопотоками в приемлемое
время диспетчерскому аппарату уже не под силу. Нужны новые средства для
усовершенствования структуры управления на железнодорожном транспорте и
создания гибкой технологии организации потоков.
Постановка
задачи. В
общем случае автоматизированная система управления состоит из информационной и
управляющей подсистем, структура которой представлена на рис. 1.
Управляющая подсистема
состоит из двух частей: решающей и проверяющей.
В решающей части находятся оптимизационные модели, позволяющие найти
оптимальную в динамике схему потоков. В качестве оптимизирующих моделей
выбираются динамические потоковые модели под общим названием «Динамическая
транспортная задача с задержками» (ДТЗЗ) [2] и ее дальнейшее развитие – «Метод
динамического согласования» (МДС) [3].
В ДТЗЗ можно учитывать:
·
ритмы работы поставщиков и потребителей;
·
стоимость доставки по направлениям;
·
сроки доставки;
·
ограничения по пропускной способности линий;
·
ограничения по перерабатывающей способности фронтов;
·
ограничения по вместимости парков путей и складов;
·
стоимости ущерба от недопоставки груза тому или иному получателю.
ДТЗЗ ставится следующим
образом: рассчитать наилучшую динамическую схему потоков, чтобы обеспечить
рациональные транспортные связи между поставщиками и потребителями в динамике.
Если в ДТЗЗ учитывается динамика производства и потребления, динамика запасов и
наличие грузов в пути, то МДС дополнительно позволяет осуществлять корректировку
программ поставщиков с целью нахождения оптимального распределения потоков
между поставщиками и потребителями. Под корректировкой в данном случае
понимается перенос производства на более ранний момент времени. Эти модели
позволяют получить оптимальную в динамике структуру потоков с учетом:
·
сокращения затрат на передвижение потоков и простои вагонов;
·
уменьшения ущерба от
недопоставки порожняка;
·
особенности структуры объекта;
·
изменения во времени основных параметров объекта;
·
изменяющихся ритмов работы фронтов погрузки и выгрузки.
Рассматриваемый далее метод
динамического согласования позволяет согласовать ритмы поставщиков и
потребителей таким образом, чтобы это соответствовало возможностям транспорта.
Ставится задача гармонической увязки в динамике в едином технологическом
процессе отправителей, получателей и транспорта. В общем случае динамической
корректировке могут подвергаться программы работы поставщиков, потребителей и
транспорта с учетом экономической целесообразности.
В проверяющей части находится имитационная
модель, которая подробно отображает работу объекта. Модель строится с помощь
имитационной системы ИСТРА [4]. Если оптимизационная модель рассчитывает схему
потоков, то имитационная проверяет реализуемость этой схемы. В случае успешной
реализации выдается решение, а в случае неудачи условия решения оптимизационной
задачи корректируются определенным образом, и процесс повторяется.
Работая
с частично-формализованными знаниями, имитационная модель воспроизводит
(имитирует) технологический процесс максимально близко к реальности, но в
ускоренном времени. Имитационная система ИСТРА позволяет строить модели
различных объектов железнодорожного транспорта – станций, узлов, полигонов,
стыковых пунктов различных видов транспорта. Модель может быть подробная –
вплоть до стрелок, локомотивов, бригад, может быть укрупненной. После имитации
технологического процесса в условиях, максимально приближенных к реальным,
выдается исчерпывающий набор количественных и качественных показателей типа
столько-то вагонов прибыло или убыло, столько-то грузов выгружено, а также
занятость путей, стрелок, локомотивов и т.п. Выдаются «узкие места» структуры и
технологии, то есть устройства и операции, вызывающие наибольшие задержки. При
необходимости выдается суточный план-график установленной формы. Модель может
строиться полуавтоматически и автоматически. При автоматическом построении,
реализованном только для сортировочных станций, система просит пользователя
сообщить параметры станции (структура потоков, число локомотивов и т.п.), и
затем описывает технологический процесс. При полуавтоматическом построении в
описании технологического процесса участвует пользователь.
Особенностью
системы ИСТРА является возможность отображения не только технологических
процессов, но и имитировать процессы передачи информации с учетом искажений и
потерь, а также иерархическое управление.
1.
Метод динамического
согласования производства и транспорта.
Этот метод рассчитывает
требуемые ритмы отправления при известных ритмах потребления и схеме
транспортной сети, чтобы обеспечить полное согласование производства и
транспорта.
Назовем струёй поток вагонов (маршрутов) между конкретным поставщиком и
потребителем. При поструйном![]() управлении потоками возникают так называемые динамические резервы
[5]. Динамическими они называются потому, что это резервы управления, и в этом
случае лишних вагонов не требуется. Соответственно фактические резервы будем
называть статическими. Рассмотрим это подробнее.
управлении потоками возникают так называемые динамические резервы
[5]. Динамическими они называются потому, что это резервы управления, и в этом
случае лишних вагонов не требуется. Соответственно фактические резервы будем
называть статическими. Рассмотрим это подробнее.
Для обеспечения надежной
транспортной связи между группой отправителей и потребителей при несовпадающих
ритмах их работы, разном расстоянии перевозки и колебании времени хода
требуются в обороте резервные вагоны с грузом. Они как демпфер будут сглаживать
неравномерность прибытия. Резервы снижают эффективность. Поструйное управление
позволяет уменьшить требуемые фактические резервы без снижения надежности
взаимодействия между отправителями и потребителями. Управление заменит резервы.
Каждый вид управления позволяет активизировать свой специфический вид резервов.
Исследовано четыре их типа [5].
Первый тип возникает при управлении
однородными потоками. Допустим, это потоки порожняка. Пусть по разным причинам
в первом пункте погрузки уменьшилась потребность в порожняке, а во втором –
увеличилась. При неизменяемой (то есть неуправляемой) схеме потоков в первом
пункте порожняк будет отставлен в резерв, а во втором взят из резерва.
Адаптивное изменение схемы потоков позволяет избежать (полностью или частично)
этих процессов. Управление заменило резервы.
Управление
неоднородными потоками активизирует динамические
резервы второго рода. Различные струи потока зачастую долго идут по одному
и тому же маршруту, используя одни и те же технические устройства. Процесс
передвижения представляет собой некую последовательность технологических
операций и межоперационных простоев. Давая «зеленую улицу» одной струе, мы как
бы перебрасываем межоперационные простои с одной струи на другую.
По
первой струе уменьшается время хода, сокращается число вагонов в движении.
Струя как бы сжимается, «выдавливая» из себя избыточные вагоны. Создается
эффект резерва. Вторая струя, напротив, поглощает дополнительные вагоны. Таким
образом, без изменения средней скорости движения потока в целом можно избежать
взятия вагонов из резерва (струя 1) и оставления их в резерв (струя 2).
Управление опять заменяет резервы.
Динамические резервы третьего рода
возникают при управляемом взаимодействии производства и транспорта. Если
возможности адаптации транспорта исчерпаны, то необходимо уменьшить рассогласование
ритмов производства и потребления (с учетом конфигурации транспортных путей).
Производственные ритмы, согласованные между собой и режимами работы транспорта
позволяют снизить требуемые фактические резервы без снижения надежности
взаимодействия.
Особый
вид представляют резервы четвертого рода.
Они возникают при адаптивном подстраивании параметров структуры транспорта к
схеме потоков. Существует целый ряд технологических способов изменения
параметров структуры – пропускной способности направлений и времени продвижения потока по ним (изменение
режима пропуска потока, добавление поездных локомотивов, изменение числа «окон»
и др.). Рассогласование в динамике схемы потоков и параметров структуры
потребовало бы создания дополнительных резервов у поставщика и потребителя.
Адаптивное согласование создает эффект резервов.
Реализовать
динамические резервы, а значит уменьшить число вагонов, занятых на перевозках,
путей под резервные вагоны, избыточный груз на колесах без специальных моделей
невозможно. Для активизации динамических резервов первого рода используется
однопродуктовая динамическая транспортная задача, второго – многопродуктовая,
третьего – метод динамического согласования производства и транспорта,
четвертого – динамическая транспортная задача с адаптивной структурой.
На
базе ДТЗЗ сформулирован метод динамического согласования производства и
транспорта. Рассмотрим его математическую модель.
Пусть
транспортная сеть состоит из P ={p1, p2,….pN} пунктов, соединенных направленными путями (pi, pj), i≠j, pi, pjÎP. Пусть [0, Т]
- интервал оптимизации функционирования
транспортной системы.
Для
каждого момента времени t(t=![]() ) на множестве P пунктов сети определена
функция производства и потребления qi(t).
Если qi(t)>0,
то пункт производства pi называется источником (пунктом производства), если qi(t)< 0,
то пункт потребления pj называется стоком (пунктом
потребления) и если qi(t)=0,
то пункт pi называется перевалочным. Каждый путь (pi, pj)
характеризуется пропускной способностью dij(t)³ 0
и транспортным запаздыванием tijÎZ0={0,1,…}. При i=j dii(t)
означает величину емкости склада пункта pi. Обозначим
через uij(t), t=
) на множестве P пунктов сети определена
функция производства и потребления qi(t).
Если qi(t)>0,
то пункт производства pi называется источником (пунктом производства), если qi(t)< 0,
то пункт потребления pj называется стоком (пунктом
потребления) и если qi(t)=0,
то пункт pi называется перевалочным. Каждый путь (pi, pj)
характеризуется пропускной способностью dij(t)³ 0
и транспортным запаздыванием tijÎZ0={0,1,…}. При i=j dii(t)
означает величину емкости склада пункта pi. Обозначим
через uij(t), t=![]() объем поставок на пути (pi, pj),
выходящий в момент t из пункта pi и приходящий в момент t+tij в пункт pj. Если путь (pi, pj) отсутствует или t+tij > T,
то полагаем uij(t)=0. Ясно, что все uij(T)=0,
i≠j. Поставка uii(t)означает
запас пункта pi в момент времени t. Поэтому tii=1. Пусть cij(t) –
расходы на перевозку единицы объема
поставок из pi. Тогда cii(t) – расходы на хранение единицы запаса.
Для каждого пункта потребления pj период, в течение которого отсутствуют
поставки, равен [0,tj-1],
где tj = min (tij), i≠j. Будем предполагать, что в момент времени t=0
существует запас ujj(0),
который обеспечит потребление в период, когда невозможны поставки, то есть
справедливо:
объем поставок на пути (pi, pj),
выходящий в момент t из пункта pi и приходящий в момент t+tij в пункт pj. Если путь (pi, pj) отсутствует или t+tij > T,
то полагаем uij(t)=0. Ясно, что все uij(T)=0,
i≠j. Поставка uii(t)означает
запас пункта pi в момент времени t. Поэтому tii=1. Пусть cij(t) –
расходы на перевозку единицы объема
поставок из pi. Тогда cii(t) – расходы на хранение единицы запаса.
Для каждого пункта потребления pj период, в течение которого отсутствуют
поставки, равен [0,tj-1],
где tj = min (tij), i≠j. Будем предполагать, что в момент времени t=0
существует запас ujj(0),
который обеспечит потребление в период, когда невозможны поставки, то есть
справедливо:
ujj
(0)+![]() qj(t) ³ 0 (2.1)
qj(t) ³ 0 (2.1)
Задача
оптимизации функционирования транспортной системы ставится как задача
минимизации суммарных транспортных расходов и расходов на хранение
J=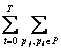 cij(t)× uij (t) (2.2)
cij(t)× uij (t) (2.2)
при ограничениях:
uii (t+1)=uii(t)+qi (t) +![]() (uji (t-tji)-uij (t)), (2.3)
(uji (t-tji)-uij (t)), (2.3)
0£ uij(t) £ dij(t);
pi, pjÎP, t=![]() , (2.4)
, (2.4)
0£ t+tij £ T, 0 £ t-tij £ T, (2.5)
uii
(0)=u0ii, uii
(T)=0, piÎP. (2.6)
Задачу (2.2 – 2.6) назовем ДТЗЗ в сетевой постановке [2.6]. Очевиден содержательный смысл ограничений. Так, уравнение (2.3) является балансным соотношением, получаемым следующими образом:
а) для отправителя:
uii(t+1)=uii(t)+qi(t) -![]() uij(t);
uij(t);
б) для получателя:
ujj
(t+1)=ujj(t)+qj (t)+![]() uij(t-tij);
uij(t-tij);
в) для перевалочного пункта:
uii (t+1) = uii(t) + ![]() uji(t-tji) -
uji(t-tji) -![]() uij(t)
uij(t)
Для
этого пункта qi(t) = 0.
Для
любого пункта получаем уравнение (2.3).
Неравенство
(2.4) означает неотрицательность поставок, ограниченных пропускными
способностями коммуникаций. Время прибытия и время отправления поставок должны
принадлежать интервалу оптимизации [0,Т], а условия (2.6) являются
начальными и конечными условиями на запасы.
Учитывая
ограничения (2.6) и суммируя по t
уравнение (2.3) получим для каждого пункта pi соотношение:
uii (0) + ![]() qi(t) +
qi(t) + ![]()
![]() (uji
(t-tji) – uij(t)) = 0. (2.7)
(uji
(t-tji) – uij(t)) = 0. (2.7)
Суммированием
по i соотношения (2.1) получаем
уравнение:
![]() u0ii +
u0ii + ![]()
![]() qi(t) = 0, (2.8)
qi(t) = 0, (2.8)
доставляющее необходимое условие разрешимости в сетевой постановке.
Теперь
перейдем непосредственно к самому МДС. Для этого введем корректирующие
переменные ωi(t) в
пунктах производства pi, означающие уменьшение qi(t) и
соответственно увеличение qi(t-1)
на величину ωi(t) с
производственными расходами ci(t)
В качестве критерия оптимальности примем экономический критерий минимума транспортных расходов, расходов на хранение и затрат на перестройку производственных программ поставщиков
J1+J2+J3→min, (2.9)
где:
J1=![]()
![]() cij(t)uij(t); (транспортные расходы) (2.10)
cij(t)uij(t); (транспортные расходы) (2.10)
J2=![]()
![]() cii(t)uii (t); (затраты на хранение
запасов) (2.11)
cii(t)uii (t); (затраты на хранение
запасов) (2.11)
J3=![]()
![]() ci(t) ωi (t); (затраты на корректировку
ci(t) ωi (t); (затраты на корректировку
программ производства) (2.12)
при ограничениях, задаваемых:
а) уравнениями динамики изменения запасов у
поставщика и динамики размещения производства:
uii (t+1) = uii(t) + qi(t)- ![]() uij(t) + ωi (t+1)- ωi (t);
uij(t) + ωi (t+1)- ωi (t);
б) уравнениями динамики изменения запасов у
потребителей:
ujj (t+1) = ujj(t) +![]() uij(t-tij) + qj(t);
uij(t-tij) + qj(t);
в) начальными и конечными условиями:
uii (0) = u0ii , ujj (T)=0, ωi(T)=0;
г) условиями неотрицательности переменных запасов,
поставок и корректирующих переменных:
uij (t)≥ 0, ωi(t)≥0.
Отметим,
что МДС позволяет менять структуру сети внутри периода [0, Т], стоимостные параметры и параметры сети также могут изменяться. Можно
согласовывать подвод разных грузов, и меняя стоимости ci(t)
при ωi(t) можно регулировать степень
перестройки ритмов отправления у разных отправителей.
Данная
задача относится к задача оперативного планирования. В предлагаемом методе с
корректировкой программ необходимые и достаточные условия разрешимости
совпадают и потому сбалансированность по объемам, как это принято, выступает в
качестве перспективного, планового показателя, а совокупность корректирующих
переменных в оптимальном решении – программа перестройки производства –
выступает в качестве оперативного показателя уже в рамках транспортной системы.
Укажем, что предлагаемая модель может быть принята за одну из возможных основ
согласования различных уровней планирования – перспективного и оперативного.
Метод
решения сводится к разложению динамического потока в статический, решению
статической транспортной задачи на сети и обратному преобразованию, но уже с
известными значениями потоков [2, 6, 7, 8].
2.
Имитационная система ИСТРА.
Под имитационной системой
понимается упорядоченный комплекс алгоритмов, программ, формальных и
неформальных процедур, позволяющий создавать имитационные модели на ЭВМ и
использовать их для решения конкретных задачах [4 ].
Создание имитационных систем
знаменует собой новый этап в использовании имитационного моделирования.
Проводимые исследования практики применения различных методов показали, что
«имитационное моделирование является одним из наиболее широко распространенных
количественных методов в решении проблем управления» [9, 10]. Преобладающее
использование имитационного моделирования объясняется тем, что оно позволяет
создавать модели на основе частично формализованных опытных, экспертных знаний, а доля таких
знаний в области транспортных систем остается довольно значительной.
К преимуществам
имитационного моделирования перед другими методами расчета можно отнести:
·
возможность наиболее полного учета взаимосвязей, действующих в системе;
·
отображение влияния внутренней структуры на характер функционирования
модели;
·
возможность неявного задания целевой функции и ограничений для сложной
системы.
Таким образом, имитационное
моделирование по сравнению с другими методами способно наиболее полно
отображать сложные транспортные системы. По мере развития характеристик
используемой при имитационном моделировании вычислительной техники появилась
возможность реализовывать модели весьма большой сложности. Так, разработанная в
УрГАПС имитационная система «ИСТРА» [4] позволяет строить модели транспортных
объектов практически любого размера и сложности.
Система ИСТРА ориентирована на исследование и
оптимизацию крупных объектов транспорта во взаимодействии с производством. При
построении системы были приняты следующие исходные предпосылки:
а) система должна
предоставлять возможность создавать модели различных видов транспорта;
б) модель должна допускать
использование частично-формализованных знаний (экспертных знаний);
в) система должна быть
проблемно ориентированной, с тем, чтобы избежать отрицательных последствий
излишней универсальности, и в то же время позволять решать достаточно широкий
круг задач заданного класса;
г) модели должны достаточно
хорошо отображать технологические и информационные процессы, а также процессы
иерархического управления;
д) необходимо достаточно
полное описание факторов случайного характера;
е) необходимость специальных
процедур, «сужающих» исходное множество вариантов и сокращающих итерационный
процесс имитационного исследования;
ж) простота входного языка и
наглядность выдаваемых результатов;
з) алгоритмы и программы
должны быть построены по модульному принципу, чтобы иметь возможность легко
расширять систему.
Система ИСТРА включает в себя универсальную абстрактную модель, способную при идентификации (параметризации) настраиваться на любой объект из заданного класса. Для этого необходимо, чтобы структурные и функциональные характеристики, значения которых отличают объекты один от другого, входили не в структуру модели и не в описание ее функции, а служили бы легко заменяемыми исходными данными для моделирования. Такими исходными данными (настроенными характеристиками) являются параметры элементов транспортной системы и связей между нами. Общая схема использования системы ИСТРА представлена на рис. 2.
Обратные связи говорят о
том, что в процессе экспериментов может возникнуть необходимость уточнения
исходных данных и даже цели исследования.
Система
позволяет формировать модели, ориентированные на решение целого ряда различных
задач, в том числе:
·
детерминированные;
·
слабоуправляемые вероятностные, близкие по принципам функционирования к
системам массового обслуживания;
·
сильноуправляемые, когда функционал задается на множестве движений
модели в пространстве состояний в явном или неявном виде (рис. 2)
Оптимизация по тому или
иному параметру осуществляется проведением ряда итерационных экспериментов с
использованием специальных процедур (типа специально разработанной процедуры
«имитационного спуска»).
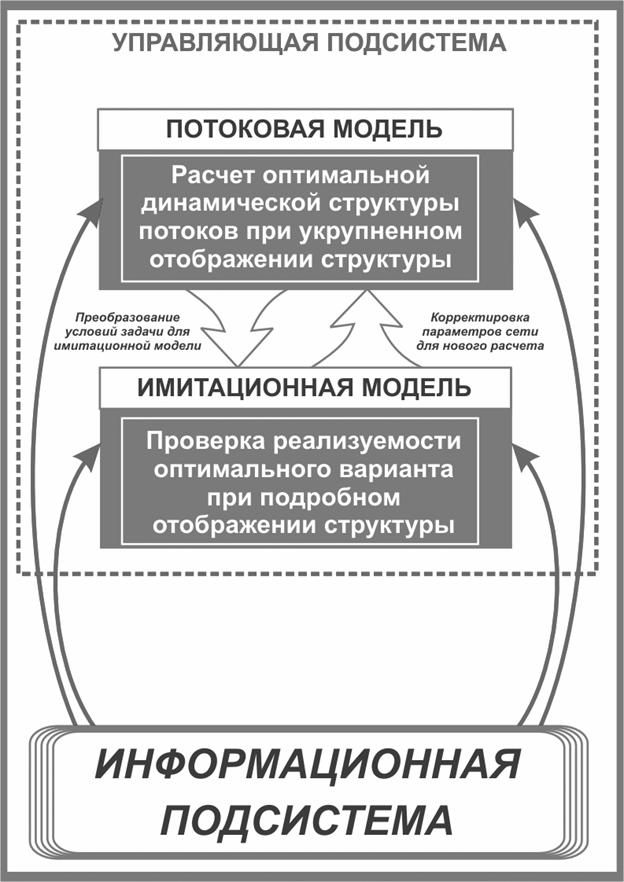
Рис. 1
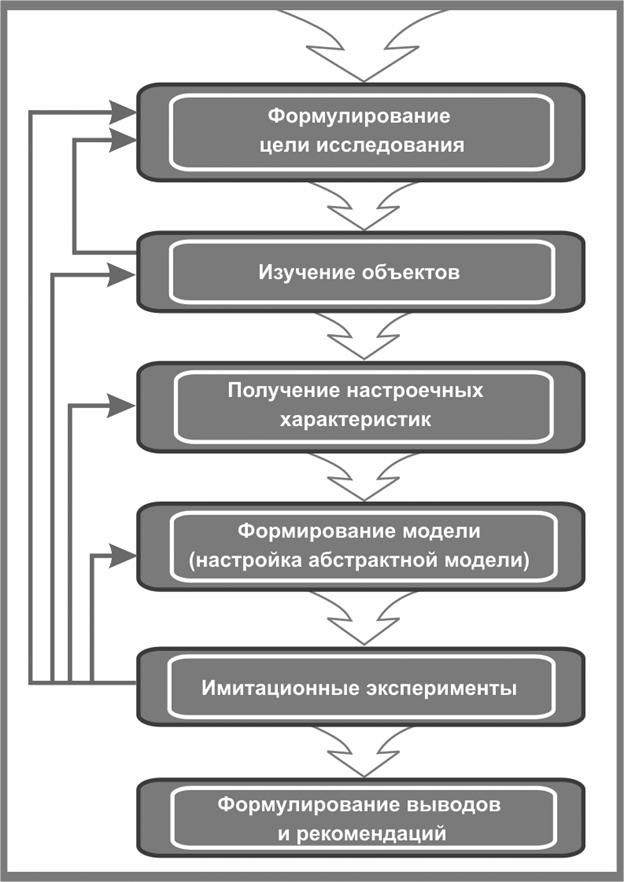
Рис. 2
Л И Т Е Р А Т
У Р А
1. Козлов П.А. Новый этап в разработке
автоматизированных систем управления.//
Автоматика, связь, информатика. М., апрель, № 5,
2. Миловидов С.П., Козлов П.А. Динамическая
транспортная задача с задержками в сетевой постановке.// Изв. АН СССР.
Техническая кибернетика. № 1,
3. Козлов П.А., Миловидов С.П. Метод динамического
согласования производства и транспорта. Вопросы комплексного развития ПТ. Труды
ИКТП, выпуск
4. Козлов П.А. Универсальная имитационная система
транспорта «ИСТРА». //Межвуз. сборник «Организация работы транспорта
промышленных предприятий» Калинин. Изд-во КГУ, 1984.
5. Козлов П.А. Активизация динамических резервов
железнодорожного транспорта при автоматизированном управлении потоками. // Сб.
трудов пятый международной конференции «ИНФОТРАНС 2000». СПб. Д102, ПГУПС,
2000.
6. Блюмин С.Л., Козлов П.А., Миловидов С.П.
Динамическая транспортная задача с задержками. //Автоматика и телемеханика, №
5, 1984.
7. Данциг Дж., Вулф Ф. Алгоритм разложения для задач
линейного программирования. // Сб. переводов «Математика», № 1, 1964.
8. Канторович Л.В., Макаров В.Л. Оптимальные модели
перспективного планирования. Применение математики в экономических
исследованиях. // Т.З. М.: Мысль, 1965.
9. Шеннон Р. Имитационное моделирование систем –
искусство и наука. // М.: Мир, 1978.
10. Аврамчук Е.Ф., Вавилов А.А., Емельянов С.В. и
др. Технология системного моделирования. //Под ред. Емельянова С.В. М.:
Машиностроение, 1988